General Theory

The determination of deformation parameters is based on the finite elements theory.

The general equation for a field of displacement can be written as

where

is the vector of displacement vectors,

is the vector of coordinates,

is the vector of translation elements, and

is the gradient of displacements, composed by symmetrical tensor of deformation and anti-symmetrical tensor of rotation .

After rearrangements we can finally express the displacements in the direction of coordinate axes by following equations

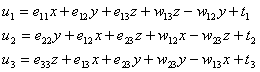
where and are the components of tensor and are the components of tensor .

The components of both tensors as well as translation in equation are unknown and can be determined by solving the system, introducing parameters for each point of displacement . Finally, the parameters of deformation,as principal axes of compression or extension, total dilatation,shear deformations and their orientation can be determined using the known formulae.

It should be stressed that the parameters of deformation do not depend on the coordinate system used, and can define the general trends of compression or extension at given area under study.

With the aim to express the deformation parameters in the plane, the approximation of field of displacement vectors was applied, using polynomials. After solving necessary equations of the following type

the values were determined as the derivatives of values for respective coordinates. After full processing, the vectors of displacement are computed and displayed in rectangular grid of an arbitrary scale. Within the same grid, the deformation parameters for each intersection can be determined.

From:

Jan Kostelecký, Milan Talich and Pavel Vyskočil: Crustal Deformation Analysis in the International Center on Recent Crustal Movements [Journal of the Geodetic society of Japan, Vol. 40, No. 4, (1994). pp, 301-308].

Full solution:

[1] Talich Milan: Using GPS Data for Deformations Analysis. 1994 IERS and IGS Workshop Paris and Saint Mandé, 1994, March 21-25, p.6.

[2] Kostelecký Jan: Výpočetní programy pro interpretaci horizontálních posunů. Technická zpráva. Zdiby: VÚGTK, 1986, 21s.

[3] Talich Milan, Kostelecký Jan, Vyskočil Pavel: Modelling of Horizontal Movements and Computing Method of Deformation Fields at the International Center On Recent Crustal Movements. In: Zpráva o řešení vědeckého projektu 4-01-60 Geodézie a dynamika Země v roce 1993, edice VÚGTK, 1993, s.104-115.

[4] Talich, Milan: Geodynamika s GPS. Sborník prací VÚGTK 1996. - Roč.41. - Zdiby: VÚGTK, 1997. - S.31-40. http://www.vugtk.cz/odis/sborniky/sb96/talich.htm