Principy výpočtů
Tenzory deformací
Základní princip výpočtu analýzy deformací z opakovaného zaměření geodetické sítě.
Na základě polohových změn bodů geodetické sítě, které jsou určeny právě jejím opakovaným zaměřením, vypočteme nejprve parametry diskrétně vyjádřeného pole posunů, což jsou posuny interpolované do čtvercové sítě a poté dále z nich vypočteme parametry opět diskrétně vyjádřeného pole deformací, charakterizované tenzory napětí (extenzí a kompresí).
Nejde o určení polohy bodů v obvyklém smyslu, jak jsou geodeti zvyklí, ale o určení jejich posunů, z nichž se poté určují deformace sítě, které budeme považovat za deformace daného vy‘etřovaného území (v případě splnění určitých podmínek pro rozmístění geodynamických bodů).
PRINCIP
Jak bylo již uvedeno vý‘e, princip užití geodetických metod spočívá v opakovaném zaměření a porovnání výsledků etap měření. Zji‘těné rozdíly v polohách bodů poté označujeme jako jejich posuny. Vyjádřeme nejprve vektor posunu bodu:
![]()
Kde x i o (resp. x i t ) je vektor souřadnic bodu P i pro základní (resp. aktuální v čase t) etapu. Tento vektor můžeme vyjádřit jako funkci souřadnic:
u = (u 1, u 2, u 3 ) T = u ( x ) = (u 1 ( x ), u 2 ( x ), u 3 ( x )) T = d, x = (x, y, z) T
Potom tenzor deformace v bodě P i je definován jako gradient této funkce v tomto bodě.
V poli pohybů platí následující vztah:
d i = E i x i + t
kde: d i je vektor posunu,
E i je gradient posunu,
x i je vektor souřadnic,
t je vektor prvků translace.
Tenzor deformace můžeme rozdělit na dvě části:
![]()
kde:
![]() je symetrický tenzor deformace,
je symetrický tenzor deformace,
![]() je antisymetrický tenzor rotace,
je antisymetrický tenzor rotace,
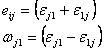
Potom můžeme psát:
![]()
Z hodnot
![]() můžeme určit velikosti parametrů deformací. Toto lze provést jednak pro 3D ře‘ení, jednak pro rovinná ře‘ení, kde touto rovinou může být např. rovina rovnoběžná s rovinou XY nebo XZ nebo YZ, nebo také obecně jakákoliv rovina lokálního souřadnicového systému do které se prostorové posuny promítnou.
můžeme určit velikosti parametrů deformací. Toto lze provést jednak pro 3D ře‘ení, jednak pro rovinná ře‘ení, kde touto rovinou může být např. rovina rovnoběžná s rovinou XY nebo XZ nebo YZ, nebo také obecně jakákoliv rovina lokálního souřadnicového systému do které se prostorové posuny promítnou.
Například pro průmět posunů do roviny XY lokálního souřadnicového systému platí :

Je důležité poznamenat, že v‘echny posuny jsou závislé na zvoleném souřadnicovém rámci. Naproti tomu v‘echny parametry deformací z posledníchrovnic, kromě směrníků ψa φ, jsou nezávislé na použitém souřadnicovém rámci. Znamená to, že pouze deformace jsou objektivním měřítkem proodhalení reálných geodynamických trendůve vy‘etřovaném území. A to takézdůvodňuje význam jejich výpočtu a užití vpraxi.
Výpočet spolehlivosti
Tenzory deformací v místech, kde je nedostatečný počet daných bodů, jsou označeny jako nespolehlivé.
Při výpočtu tenzorů deformací uživatel zadá počet ok sítě a počet bodů. Program poté počítá kolik daných bodů je ve vzdálenosti zadaných počtu ok sítě, a pokud jich je rovno nebo více než zadaný počet bodů, označí bod sítě za spolehlivý.
Výpočet na kouli
Výpočet analýzy deformací z opakovaného zaměření geodetické sítě. Prokládaná síť bodů se zadaným rozestupem má pravidelnou vzdálenost ok na kulové plo‘e a interpolace hodnot posunů na body mřížky se provádí metodou inverzní vzdálenosti. Tato metoda se používá, pokud jsou dané body v souřadnicovém systému WGS 84.
TPS
Interpolační metoda, která umožňuje vytvořit hladký povrch procházející v‘emi danými body. Tato metoda je použita pro výpočet v rovině i na kouli.
Princip výpočtu interpolace TPS ( Thin Plate Spline)
Máme danou množinu kontrolních bodů C počtu p, regularizační parametr λ

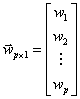
a počítáme neznámé wa a ze systému lineárních rovnic
kde K, P a O jsou submatice a w, a, v a o jsou vektory
![]()
![]()
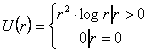
![]()
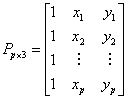 ,
,
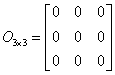
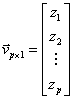 ,
,
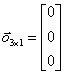 ,
,
 ,
,

Souřadnici zlibovolného bodu (x, y) na plo‘e poté můžeme vypočítat
![]()
Výpočet přesnosti pomocí metody Monte Carlo
Vstupní soubor dat musí obsahovat přesnosti daných posunů, ze kterých se poté touto metodou vypočte přesnost tenzorů deformace.
Výpočet přesnosti analyticky
Výpočet přesnosti tenzorů deformací analyticky je nyní ve vývoji
